算法

发表于

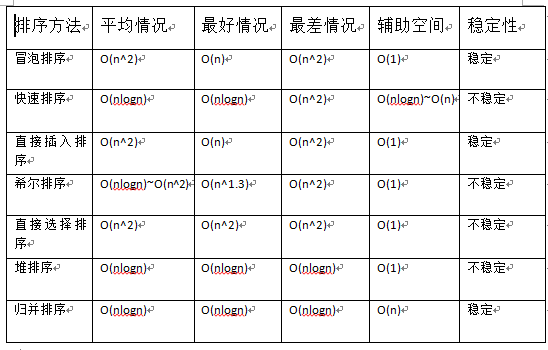
排序算法

  • 交换排序

    • 冒泡排序
    • 快速排序

  • 插入排序

    • 直接插入排序
    • 希尔(shell)排序

  • 选择排序

    • 直接选择排序
    • 堆(Heap)排序

  • 归并排序

交换排序

交换排序的基本思想都为通过比较两个数的大小，当满足某些条件时对它进行交换从而达到排序的目的。

冒泡排序

基本思想：比较相邻的两个数，如果前者比后者大，则进行交换。每一轮排序结束，选出一个未排序中最大的数放到数组后面。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

void bubbleSort(int *arr, int count)
{
    for (int i = 0 ; i < count - 1; i++) {
        printEachArr(arr, count,i);
        for (int j = 0; j < count - i - 1; j++) {
            if (arr[j] > arr[j+1]) {
                int tmp = arr[j];
                arr[j] = arr[j+1];
                arr[j+1] = tmp;
            }
        }
    }
    printEachArr(arr, count,count-1);
}

void printEachArr(int *arr, int count, int order){
    for (int i = 0; i < count; i++) {
        if (i == count - 1) {
            printf("%tu\n",arr[i]);
        } else {
            if (order >= 0 && i == 0) {
                 printf("第%tu次打印结果:%tu-",order,arr[i]);
            } else {
                printf("%tu-",arr[i]);
            }
        }
    }
}

结果：

1
2
3
4
5
6
7
8
9
第0次打印结果:5-9-7-4-10-12-3-6-1
第1次打印结果:5-7-4-9-10-3-6-1-12
第2次打印结果:5-4-7-9-3-6-1-10-12
第3次打印结果:4-5-7-3-6-1-9-10-12
第4次打印结果:4-5-3-6-1-7-9-10-12
第5次打印结果:4-3-5-1-6-7-9-10-12
第6次打印结果:3-4-1-5-6-7-9-10-12
第7次打印结果:3-1-4-5-6-7-9-10-12
第8次打印结果:1-3-4-5-6-7-9-10-12

分析：

最差时间复杂度为O(n^2),平均时间复杂度为O(n^2)。稳定性：稳定。辅助空间O(1)。

快速排序

基本思想:选取一个基准元素，通常为数组最后一个元素（或者第一个元素）。从前向后遍历数组，当遇到小于基准元素的元素时，把它和左边第一个大于基准元素的元素进行交换。在利用分治策略从已经分好的两组中分别进行以上步骤，直到排序完成。下图表示了这个过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
void swap(int * x,int *y){
    int tmp = *x;
    *x = *y;
    *y = tmp;
}

static int callCount = 0;
int partion(int *a ,int left,int right)
{
    int j = left;
    int i = j - 1;//用来指向小于基准元素的最右边的位置
    int key = a[right];//基准元素
    for(;j < right; j++){
        if(a[j] <= key){
            swap(&a[j], &a[++i]);
        }
    }
    //基准元素放在中间
    swap(&a[right], &a[++i]);
    
    callCount++;
    printQuickSort(a, 10, callCount);
    return i;
}

void quickSort(int *a, int left, int right){
    if(left >= right){return;}
    int mid = partion(a, left, right);
    quickSort(a, left, mid - 1);
    quickSort(a, mid+1, right);
}

void printQuickSort(int *arr ,int count,int n){
    printf("第%tu次打印:",n);
    for (int i = 0; i < count; i++) {
        if (i == count-1) {
            printf("%tu\n",arr[i]);
        } else {
            printf("%tu-",arr[i]);
        }
    }
}

结果:

1
2
3
4
5
6
7
8
第0次打印:5-9-7-4-10-12-3-6-1-8
第1次打印:5-7-4-3-6-1-8-10-12-9
第2次打印:1-7-4-3-6-5-8-10-12-9
第3次打印:1-4-3-5-6-7-8-10-12-9
第4次打印:1-3-4-5-6-7-8-10-12-9
第5次打印:1-3-4-5-6-7-8-10-12-9
第6次打印:1-3-4-5-6-7-8-9-12-10
第7次打印:1-3-4-5-6-7-8-9-10-12

分析:

最差时间复杂度：每次选取的基准元素都为最大（或最小元素）导致每次只划分了一个分区，需要进行n-1次划分才能结束递归，故复杂度为O(n^2)；最优时间复杂度：每次选取的基准元素都是中位数，每次都划分出两个分区，需要进行logn次递归，故时间复杂度为O(nlogn)；平均时间复杂度：O(nlogn)。稳定性：不稳定的。辅助空间：O(nlogn)。

当数组元素基本有序时，快速排序将没有任何优势，基本退化为冒泡排序，可在选取基准元素时选取中间值进行优化。

插入排序

直接插入排序

基本思想：和交换排序不同的是它不用进行交换操作，而是用一个临时变量存储当前值。当前面的元素比后面大时，先把后面的元素存入临时变量，前面元素的值放到后面元素位置，再到最后把其值插入到合适的数组位置。　

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
void insertSort(int *a,int count){
    int tmp = 0;
    printInsertSort(a, count, 0);
    for (int i = 1; i < count; i++) {
        int j = i - 1;
        if (a[i] < a[j]) {
            tmp = a[i];
            a[i] = a[j];
            while (j-1 >= 0 && tmp < a[j-1]) {
                a[j] = a[j-1];
                j--;
            }
            a[j] = tmp;
        }
        printInsertSort(a, count, i);
    }
}

void printInsertSort(int *arr,int count,int n){
    printf("第%tu次打印:",n);
    for (int i = 0; i < count; i++) {
        if (i == count-1) {
            printf("%tu\n",arr[i]);
        } else {
            printf("%tu-",arr[i]);
        }
    }
}

结果:

1
2
3
4
5
6
7
8
9
10
第0次打印:5-9-7-4-10-12-3-6-1-8
第1次打印:5-9-7-4-10-12-3-6-1-8
第2次打印:5-7-9-4-10-12-3-6-1-8
第3次打印:4-5-7-9-10-12-3-6-1-8
第4次打印:4-5-7-9-10-12-3-6-1-8
第5次打印:4-5-7-9-10-12-3-6-1-8
第6次打印:3-4-5-7-9-10-12-6-1-8
第7次打印:3-4-5-6-7-9-10-12-1-8
第8次打印:1-3-4-5-6-7-9-10-12-8
第9次打印:1-3-4-5-6-7-8-9-10-12

分析：
最坏时间复杂度为数组为逆序时，为O(n^2)。最优时间复杂度为数组正序时，为O(n)。平均时间复杂度为O(n^2)。辅助空间O(1)。稳定性：稳定。

希尔(shell)排序

基本思想为在直接插入排序的思想下设置一个最小增量dk,刚开始dk设置为n/2。进行插入排序，随后再让dk=dk/2,再进行插入排序，直到dk为1时完成最后一次插入排序，此时数组完成排序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
void shellInsertSort(int *a,int n,int dk){
    for (int i = dk ; i < n; ++i) {
        int j = i - dk;
        if (a[i] < a[j]) {
            int tmp = a[i];
            while (j>=i%dk && a[j] > tmp) {
                a[j+dk] = a[j];
                j -= dk;
            }
            a[j+dk] = tmp;
        }
    }
}

static int callCount = 0;
void shellSort(int *a, int n){
    int dk = n/2;
    printShellSort(a, n, 0);
    while (dk >= 1) {
        shellInsertSort(a, n, dk);
        dk /= 2;
        callCount++;
        printShellSort(a, n, callCount);
    }
}
void printShellSort(int *arr,int count,int n){
    printf("第%tu次打印:",n);
    for (int i = 0; i < count; i++) {
        if (i == count-1) {
            printf("%tu\n",arr[i]);
        } else {
            printf("%tu-",arr[i]);
        }
    }
}

结果:

1
2
3
4
第0次打印:5-9-7-4-10-12-3-6-1-8
第1次打印:5-3-6-1-8-12-9-7-4-10
第2次打印:4-1-5-3-6-7-8-10-9-12
第3次打印:1-3-4-5-6-7-8-9-10-12

分析:
最坏时间复杂度为O(n^2)；最优时间复杂度为O(n)；平均时间复杂度为O(n^1.3)。辅助空间O(1)。稳定性：不稳定。希尔排序的时间复杂度与选取的增量有关，选取合适的增量可减少时间复杂度。

选择排序

直接选择排序

基本思想：依次选出数组最小的数放到数组的前面。首先从数组的第二个元素开始往后遍历，找出最小的数放到第一个位置。再从剩下数组中找出最小的数放到第二个位置。以此类推，直到数组有序。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
void selectSort(int *a, int count){
    for (int i = 0; i < count; i ++) {
        printSelectSort(a, count,i);
        int key = i;
        for (int j = i + 1; i < count; j++) {
            if (a[j] < a[key]) {
                key = j;
            }
        }
        if (key != i) {
            int tmp = a[key];
            a[key] = a[i];
            a[i] = tmp;
        }
    }
}

void printSelectSort(int *arr, int count, int n){
    printf("第%tu次打印:",n);
    for (int i = 0; i < count; i++) {
        if (i == count-1) {
            printf("%tu\n",arr[i]);
        } else {
            printf("%tu-",arr[i]);
        }
    }
}

结果:

1
2
3
4
第0次打印:5-9-7-4-10-12-3-6-1-8
第1次打印:5-3-6-1-8-12-9-7-4-10
第2次打印:4-1-5-3-6-7-8-10-9-12
第3次打印:1-3-4-5-6-7-8-9-10-12

分析:
最差、最优、平均时间复杂度都为O(n^2)。辅助空间为O(1)。稳定性：不稳定。

堆(Heap)排序

基本思想：先把数组构造成一个大顶堆（父亲节点大于其子节点），然后把堆顶（数组最大值，数组第一个元素）和数组最后一个元素交换，这样就把最大值放到了数组最后边。把数组长度n-1,再进行构造堆，把剩余的第二大值放到堆顶，输出堆顶(放到剩余未排序数组最后面)。依次类推，直至数组排序完成。

下图为堆结构及其在数组中的表示。可以知道堆顶的元素为数组的首元素，某一个节点的左孩子节点为其在数组中的位置2，其右孩子节点为其在数组中的位置2+1，其父节点为其在数组中的位置/2（假设数组从1开始计数）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
void createBigHeap(int a[],int i, int n)
{
    for (; i >= 0; i--) {
        int left = 2*i + 1;//左节点
        int right = 2*i + 2;//右节点
        int j = 0;
        
        //找到左右节点中较大的那个
        if (right < n) {
            if (a[left] < a[right]) {
                j = right;
            } else {
                j = left;
            }
        } else {
            j = left;
        }
        
        //子节点大于父节点时，交换
        if (a[j] > a[i]) {
            int tmp = a[i];
            a[i] = a[j];
            a[j] = tmp;
        }
    }
}

void heapSort(int *a,int n){
    //如果有n个元素 那么最后一个非叶子节点为n/2-1
    createBigHeap(a, n/2 - 1 , n);//创建大顶堆
    printHeapSort(a, n, 0);
    for (int j = n - 1; j >= 0; j--) {
        int tmp = a[0];
        a[0] = a[j];
        a[j] = tmp;
        
        int i = j /2 - 1;
        createBigHeap(a, i, j);
        printHeapSort(a, n, n-j);
    }
}

void printHeapSort(int *arr, int count, int n){
    printf("第%tu次打印:",n);
    for (int i = 0; i < count; i++) {
        if (i == count-1) {
            printf("%tu\n",arr[i]);
        } else {
            printf("%tu-",arr[i]);
        }
    }
}

结果:

1
2
3
4
5
6
7
8
9
10
11
第0次打印:12-10-5-6-9-7-3-4-1-8
第1次打印:10-8-7-6-9-5-3-4-1-12
第2次打印:9-1-7-6-8-5-3-4-10-12
第3次打印:8-4-7-6-1-5-3-9-10-12
第4次打印:7-6-3-4-1-5-8-9-10-12
第5次打印:6-5-3-4-1-7-8-9-10-12
第6次打印:5-1-3-4-6-7-8-9-10-12
第7次打印:4-1-3-5-6-7-8-9-10-12
第8次打印:3-1-4-5-6-7-8-9-10-12
第9次打印:1-3-4-5-6-7-8-9-10-12
第10次打印:1-3-4-5-6-7-8-9-10-12

分析:

最差、最优‘平均时间复杂度都为O(nlogn)，其中堆的每次创建重构花费O(lgn)，需要创建n次。辅助空间O（1）。稳定性：不稳定

归并排序

基本思想：归并算法应用到分治策略，简单说就是把一个答问题分解成易于解决的小问题后一个个解决，最后在把小问题的一步步合并成总问题的解。这里的排序应用递归来把数组分解成一个个小数组，直到小数组的数位有序，在把有序的小数组两两合并而成有序的大数组。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
void merge(int *a,int left,int mid,int right){
    int len = right - left + 1;
    // 动态分配内存空间，如果失败就退出程序
    int *tmp = (int*)malloc(len*sizeof(int));
    int k = 0;
    int i = left;
    int j = mid + 1;
    while (i <= mid && j <= right) {
        tmp[k++] = a[i] < a[j] ? a[i++] : a[j++];
    }
    
    while (i <= mid) {
        tmp[k++] = a[i++];
    }
    
    while (j <= right) {
        tmp[k++] = a[j++];
    }
    
    for(int k = 0; k < len; k++){
        a[left++] = tmp[k];
    }
}

static int callCount = 0;
static int n = 0;
void mergeSort(int *a,int left,int right){
    if (left >= right) {
        return;
    }
    if (callCount == 0) {
        n = left + right + 1;
        printMergeSort(a, n, 0);
    }
    callCount++;
    int mid = (left + right) / 2;
    mergeSort(a, left, mid);
    mergeSort(a, mid+1, right);
    merge(a, left, mid, right);
    
    printMergeSort(a, n, callCount);
}

void printMergeSort(int *arr, int count, int n){
    printf("第%tu次打印:",n);
    for (int i = 0; i < count; i++) {
        if (i == count-1) {
            printf("%tu\n",arr[i]);
        } else {
            printf("%tu-",arr[i]);
        }
    }
}

结果：

1
2
3
4
5
6
7
8
9
10
第0次打印:5-9-7-4-10-12-3-6-1-8
第4次打印:5-9-7-4-10-12-3-6-1-8
第4次打印:5-7-9-4-10-12-3-6-1-8
第5次打印:5-7-9-4-10-12-3-6-1-8
第5次打印:4-5-7-9-10-12-3-6-1-8
第8次打印:4-5-7-9-10-3-12-6-1-8
第8次打印:4-5-7-9-10-3-6-12-1-8
第9次打印:4-5-7-9-10-3-6-12-1-8
第9次打印:4-5-7-9-10-1-3-6-8-12
第9次打印:1-3-4-5-6-7-8-9-10-12

参考

七大经典排序算法总结(C语言描述)

What is a plain English explanation of “Big O” notation?